Topology optimization determines the distribution of material most suitable to a given objective. It is primarily used to produce a fundamental basis for the engineers at the conceptual design stage, or to generate ideas for new alternatives.
In order to express the distribution of materials in topology optimization, density variables of the finite elements created for analysis are used. The element density of 1 represents a part that requires the element, while 0 represents a part that does not require the element. Unlike parametric optimization, the only design variable is the element’s density. As such, the user does not specify separate design variables but composes an optimization problem using only the combinations of objective functions and constraints.
Like any optimization problem, Topology optimization includes the following fundamental elements:
Objective: In this problem, the objective is to minimized the static compliance (a function of element density expressed in the form of global deformation energy):

Where:
f : Load vector
u : Global & element displacement vectors
K: Global & element stiffness matrices
Design variables: Volume fraction (the n_nodes density values which determine whether material is present (1) or absent (0))
Geometric constraints: the initial unoptimized geometry:
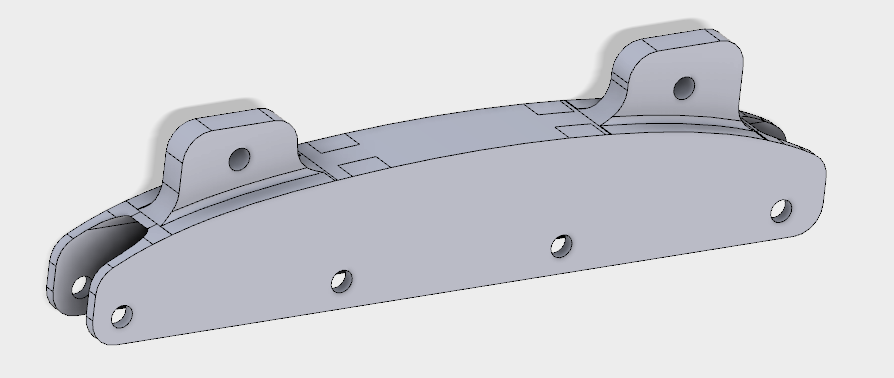
Design evaluator: the linear elasticity solver of MidasNFX, that calculates deformation energy based on specified loads and boundary conditions.
Since we are looking for general guidelines of an optimal design (in practice, we should say “better design”), the next step consists of modifying the original CAD geometry to remove material when it’s not needed:
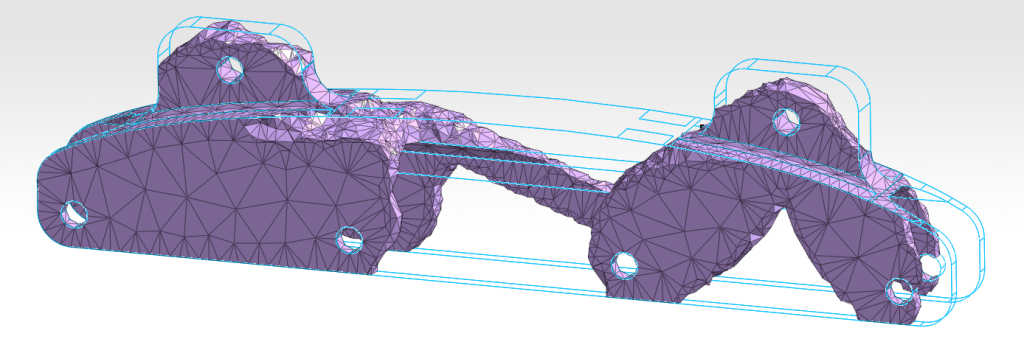

Topology optimization often leads to complicated organic-like products that cannot be manufactured using traditional processes (which is not necessarily the case here). Additive manufacturing, like 3D printing, is sometimes more adapted for this kind of design. Here, a printed version of the optimized part is produced.
This video summarizes the whole process:

